Non-Global Field-Of-View Orthographic Map Projection
Each time I return from travelling I like to make a map of all the places that I have been. Each year I usually post a blog with an updated map, such as the blog post from January this year. That previous blog post contains a global map using the Robinson projection with a scatter plot of all of the geo-tagged photos that I have taken (the Cartopy documentation contains a nice list of all of the map projections available).
Recently I have written a function pyguymer3.geo.create_map_of_points() which makes a nice map of all of the geo-tagged photos from a single trip. This way it is much easier to see where I have been in a particular part of the world. Unfortunately, this raises an age old question: “what map projection should I use?” I personally like top-down projections as a way of reducing distortion in the centre of the map and as a way of making the peripheral distortion symmetric.
The second and third questions this then raises are: “where is the centre of some photos?” and “what is the field-of-view of the map?” It turns out that finding the centre of a collection of points (which minimises the maximum distance from the centre back out to any of the points) is a hard mathematic problem (called the smallest-circle problem). I have written a function pyguymer3.geo.find_middle_of_locs() which does just that. The function returns the central longitude and latitude of some points as well as the radius of the circle from the central point which encompasses all of the points. The function has four different methods for finding the centre, with the “GeodesicCircle” method being “the best” and probably the one that the user wants normally. I am quite proud of this method: it picks a starting location by simply finding the centre of the Euclidean bounding box and then calculates the gradient of the maximum Geodesic distance to all of the points; it then iterates and walks down the slope (assuming that the local minimum is the global minimum) and stops once it has converged the location of the centre to minimise the maximum Geodesic distance to all of the points.
Using my recent holiday to Australia and New Zealand as a worked example, here is a comparison of the centres and field-of-views of the four different methods:
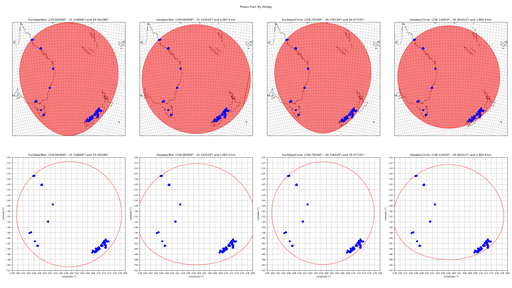
You can see that the two Euclidean methods appear as circles in Euclidean space and as skewed ellipses in Geodesic space. Conversely, the two Geodesic methods appear as skewed ellipses in Euclidean space and as circles in Geodesic space. You can also see that the two “Circle” methods produce slightly shifted centres and slightly smaller field-of-views than their respective “Box” methods.
How good is the assumption that the initial gradient of the surface will lead you to the global minimum? The below plot shows how smoothly varying the surface is for this one worked example:
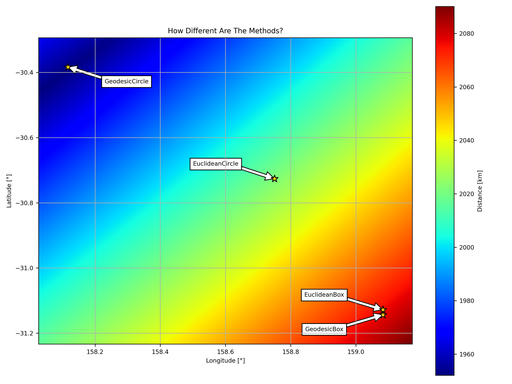
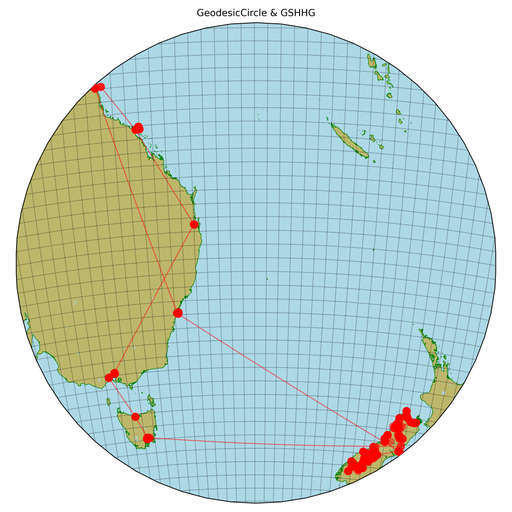
The field-of-view using the “GeodesicBox” method is 2,087.0 km and for the “GeodesicCircle” method this reduces to 1,962.9 km. This is most noticeable if you look at the south-east quadrant of the red circle: the two “Box” methods have a large gap between the red circle and the nearest photo whereas the two “Circle” methods have a photo right on the red circle.
In the earlier maps, I like the appearance of the top row of maps - they allow the viewer to see all of the points, especially the ones near the periphery. There are two map projections in Cartopy which are top-down views of a location on the surface of the Earth: the cartopy.crs.NearsidePerspective projection; and the cartopy.crs.Orthographic projection. Out of those two projections, only the cartopy.crs.NearsidePerspective projection allows the user to have a non-global field-of-view (by allowing the user to set the altitude that the camera is above the surface of the Earth). Continuing to use my recent holiday to Australia and New Zealand as a worked example, here is the cartopy.crs.NearsidePerspective representation of all of the photos that I have taken:
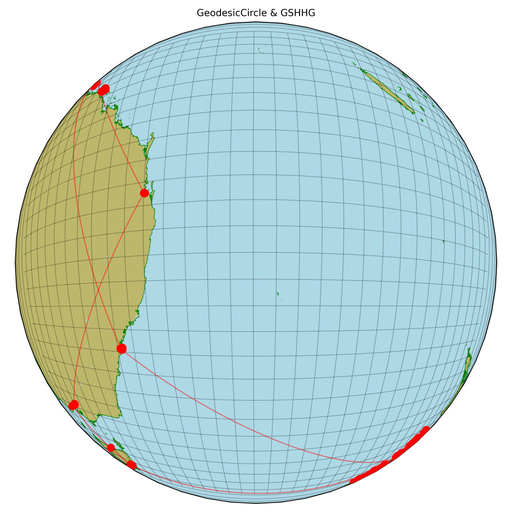
I strongly dislike the above map projection because I believe that the distortion around the periphery is too high. I would like a map projection which has the same field-of-view but a reduced magnification of the centre and an increased magnification of the periphery. The cartopy.crs.Orthographic projection looks nice but it has no user argument to reduce the field-of-view: enter my function pyguymer3.geo._add_topDown_axis()! The function pyguymer3.geo._add_topDown_axis() manually sets the axes limits to fool Cartopy in to only showing a small central region of the full cartopy.crs.Orthographic projection. This produces much prettier results in my opinion:
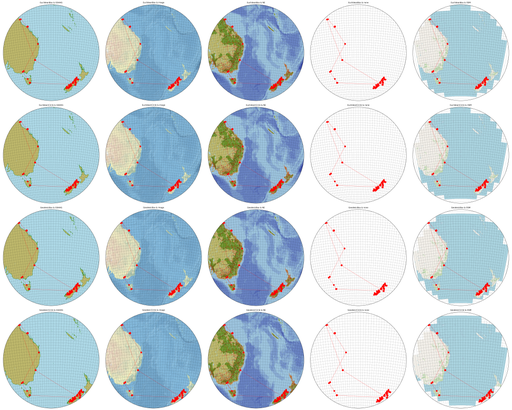
My function pyguymer3.geo.create_map_of_points() offers five different options for the background of the map which, coupled with the four different methods for determining the centre and the field-of-view, results in twenty different possible maps:
I wonder what all this says about me? As always, there is a relevant xkcd about this: